Teoría de numeros binarios

 NUMEROS BINARIOS

El sistema binario, llamado también sistema diádico en ciencias de la computación, es un sistema de numeración en el que los números se representan utilizando solamente las cifras cero y uno (0 y 1). Es uno de los que se utiliza en las computadoras, debido a que trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).

CONVERSIÓN ENTRE BINARIO Y DECIMAL

Decimal a binario

Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2. Es decir, cuando el número a dividir sea 1 finaliza la división.

Ejemplo

Transformar el número decimal 100 en binario.

BINARIO A DECIMAL

Para realizar la conversión de binario a decimal, realice lo siguiente:

1. Inicie por el lado derecho del número en binario, cada cifra multiplíquela por 2 elevado a la potencia consecutiva (comenzando por la potencia 0, 2⁰).
2. Después de realizar cada una de las multiplicaciones, sume todas y el número resultante será el equivalente al sistema decimal.

Ejemplo

El número binario 1010010 corresponde en decimal al 82. Se puede representar de la siguiente manera:





entonces se suman los números 64, 16 y 2:

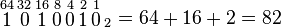
Sistema binario a octal

Debido a que el sistema octal tiene como base 8, que es la tercera potencia de 2, y que dos es la base del sistema binario, es posible establecer un método directo para convertir de la base dos a la base ocho, sin tener que convertir de binario a decimal y luego de decimal a octal. Este método se describe a continuación:
Para realizar la conversión de binario a octal, realice lo siguiente:

1) Agrupe la cantidad binaria en grupos de 3 en 3 iniciando por el lado derecho. Si al terminar de agrupar no completa 3 dígitos, entonces agregue ceros a la izquierda.

2) Posteriormente vea el valor que corresponde de acuerdo a la tabla:
 

3) La cantidad correspondiente en octal se agrupa de izquierda a derecha.

Ejemplo

• 110111 (binario) = 67 (octal). Proceso:

111 = 7
110 = 6
Agrupe de izquierda a derecha: 67

Octal a binario

Cada dígito octal se convierte en su binario equivalente de 3 bits y se juntan en el mismo orden.

Ejemplo

247 (octal) = 010100111 (binario).
El 2 en binario es 10,
pero en binario de 3 bits es Oc(2) = B(010)
 el Oc(4) = B(100)
 y el Oc(7) = (111)
 luego el número en binario será 010100111.

Binario a hexadecimal

Para realizar la conversión de binario a hexadecimal, realice lo siguiente:

1) Agrupe la cantidad binaria en grupos de 4 en 4 iniciando por el lado derecho. Si al terminar de agrupar no completa 4 dígitos, entonces agregue ceros a la izquierda.

2) Posteriormente vea el valor que corresponde de acuerdo a la tabla: 

3) La cantidad correspondiente en hexadecimal se agrupa de derecha a izquierda.

Ejemplo

• 110111010 (binario) = 1BA (hexadecimal). Proceso:

1010 = A
1011 = B
1 entonces agregue 0001 = 1
Agrupe de derecha a izquierda: 1BA

PRÁCTICAS EN CLASE DE BINARIOS

  http://karnportafolio.blogspot.com/p/blog-page_28.html